Work and Energy

Work Done by a Constant Force

The work done by the constant force F acting on an object is the dot product of the magnitude of force and the distance traveled in parallel direction by the object when the force is applied.

Forces that work/ do not work

Positive and Negative Work

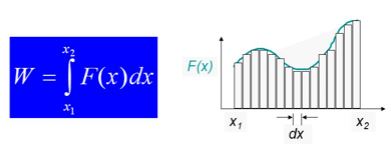
Work Done by a Variable Force

On a graph of force as a function of position, the total work done by the force is represented by the area under the curve between the initial and final positions.

Energy

Energy is the quantitative property that must be transferred to an object in order to perform work on, or to heat, the object. Energy is a conserved quantity; the law of conservation of energy states that energy can be converted in form, but not created or destroyed.

Kinetic Energy

The kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity.

Expression for Kinetic Energy

Source: http://hyperphysics.phy-astr.gsu.edu

Potential Energy

1. Gravitational Potential Energy

2. Elastic Potential Energy

Elastic potential energy is the energy stored in an object that is stretched or compressed. Elastic potential energy can be stored in the elastic objects such as springs, rubber bands etc.

Work done on stretching a spring

Source: http://slideplayer.com

Work-Energy Theorem

Net work on an object causes a change in the kinetic energy. The work done in a body due to a force is equal to the change in its kinetic energy.

i.e. Work done = Change in Kinetic Energy

Principle of Conservation of Energy

Question: With what speed must a ball be thrown down for it to bounce 10m higher than its original level? Assume no energy loss in striking the ground.

Answer:

  

Let, height of ball before throwing (h₁)                      = x m

So, height of ball after bounce on ground (h₂)           = (x +10) m

If there is no loss of energy in striking the ground by ball, then from principle of conservation of energy,

Energy on ball while throwing            = Energy on ball at maximum height after bounce

Potential Energy + Kinetic Energy     = Potential energy at maximum height after bounce

mgh₁    +          ½ mv² = mgh₂

Where, ‘m’ is mass of ball, ‘g’ is acceleration due to gravity and ‘v’ is the velocity with which ball is thrown.

Or,                  m (g x + ½ v²)             = mg (x + 10)

Or,                   gx + ½ v²                     = gx + 10 g

Or,                   ½ v²     = 10 × 9.8

Or,                   v²         = 2× 10× 9.8.  = 196

Or,                   v = 14 m/s

So, the ball must be thrown with 14 m/s to have 10m higher height attained after bounce on ground.

Conservative Forces and Non-conservative Forces

Power

Collisions

A collision occurs when two or more objects hit each other. When objects collide, each object feels a force for a short amount of time.

Elastic Collisions

An elastic collision is a collision in which there is no net loss in kinetic energy in the system as a result of the collision. Both momentum and kinetic energy are conserved quantities in elastic collisions.

Elastic Collision in One Dimension

Source: http://www.citycollegiate.com

Since the collision is elastic, so the K.E of the system before and after collision is conserved .

Dividing equation (2) by equation (1) to find v1 and v2 and putting their values in equation (1) respectively If the masses of colliding bodies are equal, i.e. m1 = m2 , v1 = u2 and v2 = u1 . After an elastic collision, the velocities of the colliding bodies are mutually interchanged.

Inelastic Collision

An inelastic collision is a collision in which there is a loss of kinetic energy. While momentum of the system is conserved in an inelastic collision, kinetic energy is not. This is because some kinetic energy had been transferred to something else. Thermal energy, sound energy, and material deformation are likely culprits.

Inelastic Collision in One Dimension

Source: http://hydrogen.physik.uni-wuppertal

Coefficient of Restitution